Solo uno scherzo?
Come è possibile che un modesto amatore, capace di correre la maratona a 4’10 al km, possa sconfiggere l’atleta forse più forte della storia della distanza regina? Chiaramente sono ironico quando affermo di poter tagliare il traguardo prima di Kipchoge, ma nel contempo sono anche estremamente serio.
Conosco realmente un modo per sconfiggere l’unico uomo capace di correre di 42,195km in meno di 2 ore. Come sostengo nel titolo, mi basta unicamente che il campione keniano mi conceda 100 metri di vantaggio.
Non è necessario che Kipchoge sia infortunato, acciaccato o abbia delle limitazioni particolari. Può correre al massimo delle sue possibilità. Mi bastano solo 100 metri di vantaggio.
I dati concreti
No, non sono pazzo. So che la mia affermazione è assurda se letta unicamente a un livello materiale. Se io e Kipchoge corressimo realmente insieme e io godessi di un vantaggio di 100 metri, dopo pochi minuti dallo Start sarei già stato sorpassato e da quel momento in poi non mi rimarrebbe che vedere la distanza che ci separa crescere.
Sconfiggere Kipchoge con la logica
Però se da livello puramente materiale, mi sposto in ambito filosofico e chiedo aiuto ai paradossi della logica, io effettivamente posso tagliare il traguardo di una maratona prima di Kipchoge se mi vengono dati 100 metri di vantaggio. Come è possibile?
Il paradosso di Zenone: Achille e la tartaruga
Zenone di Elea è stato un filosofo greco vissuto nel V secolo a.C., allievo di Parmenide. Si pensa abbia scritto una quarantina di paradossi, seppure ai giorni nostri noi ne siano arrivati soltanto due. Questi si rifanno all’argomento del movimento ed il più conosciuto è quello di Achille e la tartaruga.
Nella mia sfida con Kipchoge chiaramente io vestirò i panni della tartaruga ed il campione keniano quelli di Achille.
Chiaramente è ovvio che Achille, nella realtà che conosciamo, recupererà velocemente la tartaruga e la supererà, ma il bello dei paradossi è il saper sovvertire le regole vigenti nel mondo.
La spiegazione del paradosso
Per comprendere il paradosso dobbiamo concentrarci specificamente sui 100 metri che separano la tartaruga (io) e Achille (Kipchoge). Per percorrere questa distanza X1 avremo bisogno di un dato tempo T1.
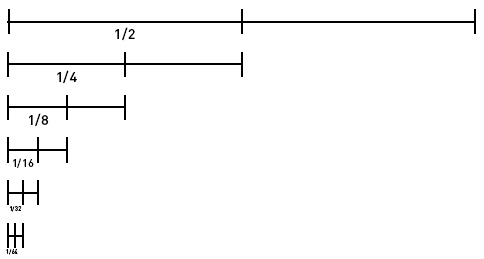
Ora immaginiamo di dividere i 100 metri in due parti. Abbiamo ore una distanza X2, 1/2 della distanza originaria, che richiederà un tempo T2 per essere percorsa. La distanza X2 potrà essere a sua volta divisa e diventerà 1/4 di quella iniziale.
Ogni distanza può essere espressa in frazione.
Ogni frazione può essere suddivisa in una frazione più piccola. Sempre. Le distanze, così concepite, comprese nei 100 metri di distanza tra la tartaruga (io) e Achille (Kipchoge) sono quindi infinite. Esisterà sempre una frazione in cui dividere la precedente
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 …….
Cosa ne consegue?
Conclusione
Giocando con il paradosso di Zenone e applicandolo alla maratona, io posso battere senza grande sforzo Kipchoge al massimo delle sue potenzialità.
Chiaramente non ho mai nemmeno lontanamente pensato di sfidare realmente il campione keniano, inavvicinabile per un modesto amatore, quale io sono. Volevo solo divertirmi un pò. Spero non mi abbiate preso troppo sul serio e di essere riuscito a strapparvi un sorriso, anche beffardo, ma pur sempre un sorriso.
Buone corse.
Per approfondimenti
- Il libro di Vincenzo Fano sui Paradossi di Zenone;
- Il libro di Mazur su Achille e la Tartaruga ed i paradossi del moto.